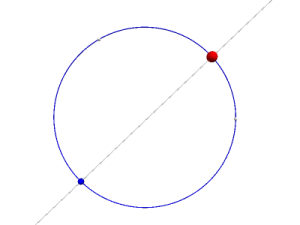
CircleAntiPodal
point on the given circle diametrically opposite to the given point
constructors:- CircleAntiPodal (circle,point )
- AntiPodal (circle,point )
inherits
_Point
Methods defined in CircleAntiPodal
Methods defined in _Point
Methods defined in Position3
f toInterpolated(self, p1, p2, r) ...
set the position on a line connecting to given points, based on the interpolation by a given ratio of the distance between the given points
f toCentroid(self, p1, p2, p3) ...
move to the centroid of the triangle defined by the 3 point arguments
f toOrthoCenter(self, p1, p2, p3) ...
move to the orthocenter of the triangle defined by the 3 point arguments
f toInCenter(self, p1, p2, p3) ...
move to the center of the circle inscribed in the triangle defined by the 3 point arguments
f toExCenter(self, p1, p2, p3) ...
move to the excenter of the circle exscribed in the triangle defined by the 3 point arguments, and tangent to the side opposite the first point argument
f toOpposite(self, object, point) ...
set postion as antipodal to the given point relative to the given object, i.e. circle or sphere
f toInterSection(self, p11, p12, p21, p22, test=True) ...
set position as the intersection of the line connecting the 1st and 2nd point arguments with that connecting the 3rd and 4th point arugments. Default is to test if lines are slew
f toPlaneIntersection(self, plane, p1, p2, test=False) ...
set to position of intersection of given plane with the line connecting the point arguments. Default is not to test if line is on plane
f toPlaneReflection(self, u, d) ...
move to the reflection of the current position in the plane defined by the 3 element vector representing the planes unit normal and a numeric value representing the plane's distance from the origin
f toSphereCenter(self, p1, p2, p3, p4) ...
set position as the center of the sphere defined by the 4 given points
f toCircumCenter(self, p1, p2, p3) ...
set position as the center of the circle on the 3 given points
f toBisector(self, p1, p2, p3) ...
set position the (interior) bisector of the angle at the 1st point argument formed with the the 2nd and 3rd point arguments
f toExtBisector(self, p1, p2, p3) ...
set position the exterior bisector of the angle at the 1st point argument formed with the the 2nd and 3rd point arguments
f toInvertPoint(self, circle, p1) ...
set position as the inversion of the given point in the given circle, on the circle's plane
f toCrossPoint(self, p1, p2, p3, p4, p1a, p2a, p3a) ...
set position as the crosspoint (equating cross ratios) of the last 3 (ordered) points with the first 4 (ordered) points
f toCircumPoint(self, circle, rad) ...
rotate the current position (assumed to be on the circle's circumference) by the given angle, in radians
f toHarmonic(self, p1, p2, p3) ...
set position as the harmonic with of the 3rd point argument with reespect to the 1st and 2nd point arguments
Methods defined in vector
Methods defined in Element
f _togglenull(self) ...
toggle the 'null' flag, indicating whether the current postion of the object's position is visible - e.g. is real when working in real space
Methods defined in drawPoint
f draw(self) ...
For consistency in iterating Element's rendering objects, all elements rendering information is in a list called self.rend. In the case of Points, it is either a single element list, containing a cvisual sphere object, or a 2 element list with each element an oriented cvisual pyramid object, which together form a diamond shape representing the point
Attributes
a __opts__
['color', 'initcolor', 'trace', 'level', 'texture', 'extend', 'povout', 'label', 'append', 'export', 'pointsize', 'tracewidth', 'tracecolor', 'maxtrace', 'mintrace', 'fontsize', 'fontcolor', 'fontXofffset', 'fontYofffset', 'style']
a __doc_hints__
{'args': ['circle,point'],
'conditions': ['point and circle are coplanar', 'point not circle center'],
'factory': 'AntiPodal',
'otherwise': 'None ; None'}
See the source for more information.